Designs
I've had to make a lot of art for my articles and videos. Here's some of what I consider to be my best work. You'll find rest of it in my articles and on my YouTube channel.
Given that it's my icon, I should probably start with this one. It's an earlier version of what would be my icon, but it's animated. In it, we use a construction of the pentagon associated with Albrecht Dürer. We follow the standard rules of using a compass and straightedge. I picked this construction because I found it particularly pleasing with its symmetry. You can read more about constructability in my article What is a Field in Abstract Algebra, in which I talk about how fields solved a mystery that had been puzzling geometers for millennia.

This animation indicates the paths light would take if it ran into a medium with a higher refractive index. Here, I'm using both the hue and brightness of the color itself to emphasize the minimum path. You can see it in context in The Principle of Least Action, where these paths represent the paths I ask the reader to integrate along to verify Snell's Law.

This image represents a few iterations in a cellular automata I came up with back in High School. At the time, I wanted to know about how long it would go before it would repeat along with how long the cycles would last, but I didn't know how to analyze it at the time. After I graduated from college, I looked back and tried some stuff before I realized that I had the tools to figure this system out. I started working on it and I realized that it might be a good series to write about, so I started working on my second major series: How to Discover Finite Fields While Bored in Class. In the series, I explain the mathematical concepts in Abstract Algebra and Linear Algebra that lead to some crazy results.
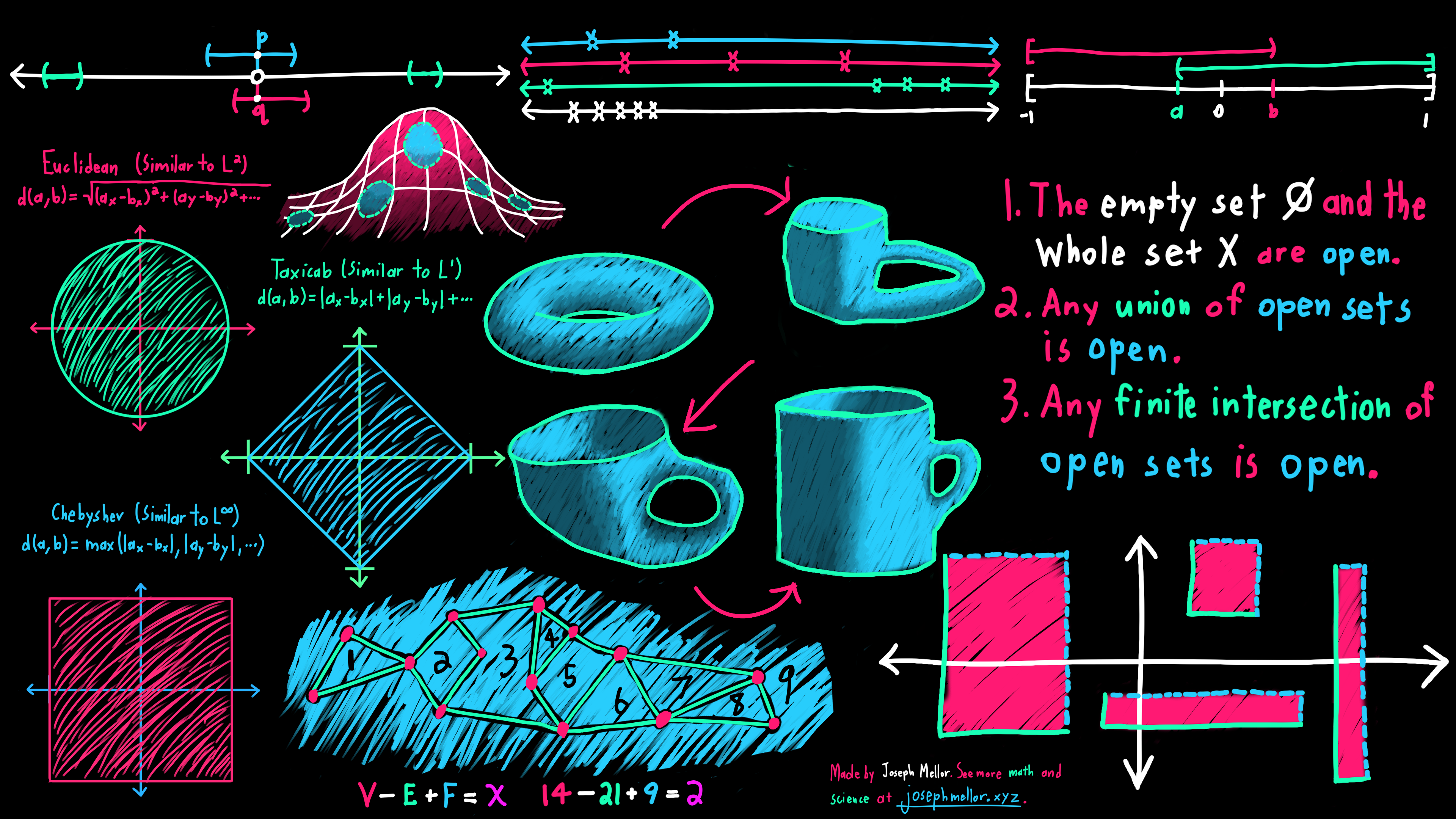
This is the featured image for my article An Intro to Topology. It's a collage of the best work in probably the most artistic article I've written (the other contenders are either The Generalized Stokes' Theorem or Fields in Abstract Algebra, both of which fill out this list).
This video is a neat little demonstration that the Mobius strip is not orientable, which means that it's possible to travel along it and end up back where you started, but flipped. It's particularly important for The Generalized Stokes' Theorem because you non-orientability means that things don't cancel and the proof breaks down. Its non-orientability means it's also pretty annoying to work with in any digital program, but I figured it out.
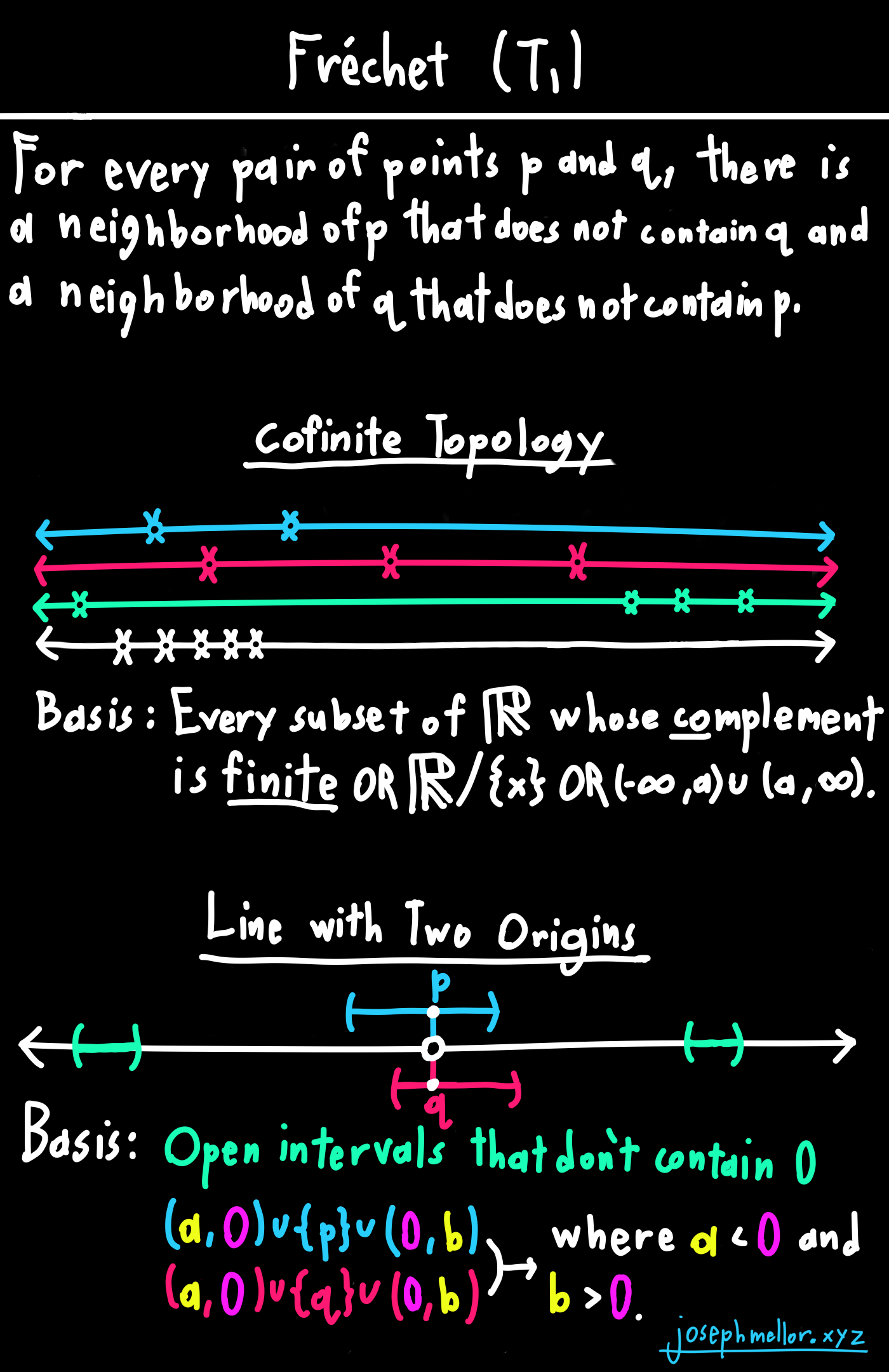
This image is my favorite of the several cards I made for the separation axioms in my article An Intro to Topology. It's clean, it gets the point across, the color scheme is great, my handwriting is great, etc.
Sometimes, it's good to keep it simple, and this animation is a prime example. This video shows off the standard coordinate systems by showing how the point moves in space as you change the coordinates. There's nothing going on here except moving a point through space. I do like the color scheme, though. I made it for Intro, Coordinates, and Kinematics, the first article in my series The Road to Quantum Mechanics.
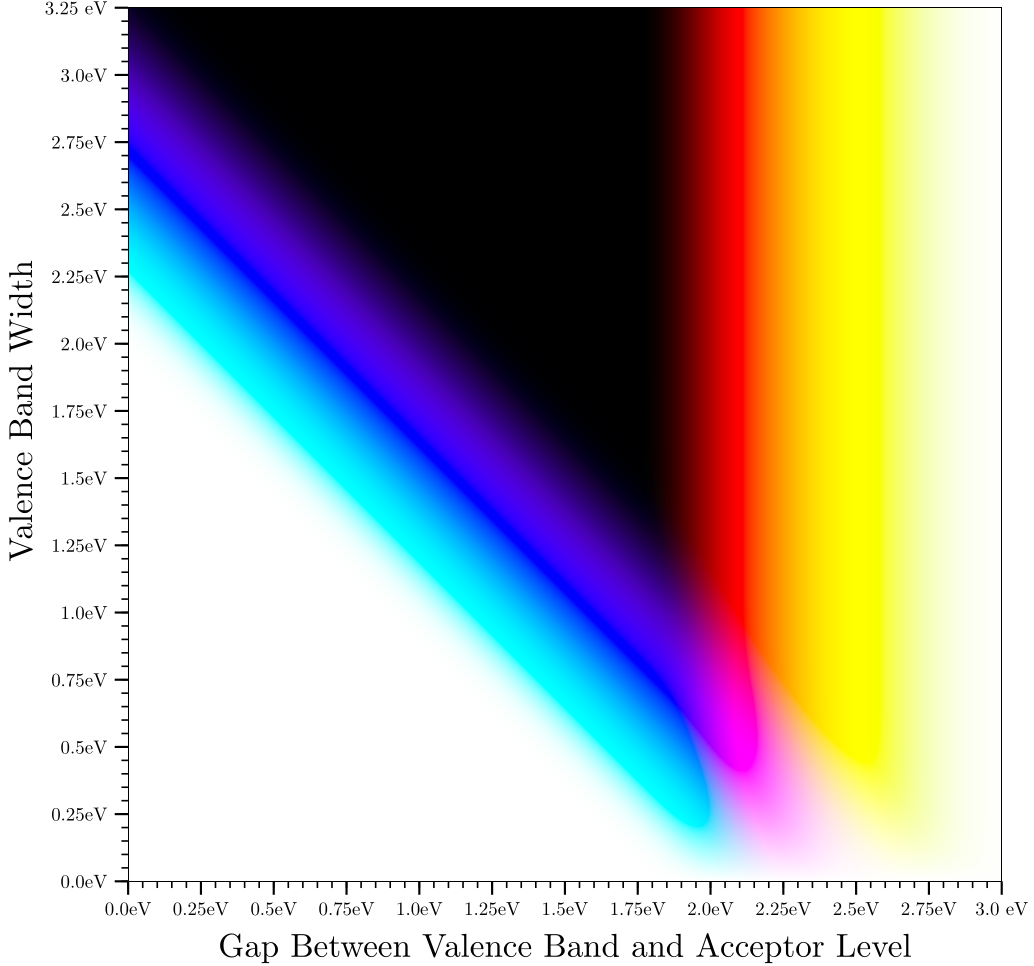
I won't be able to give a full explanation here, (so check out my article A Layman's Intro to Material Science), but this image shows the approximate color of a material given a simplified model of its band gap. Here, I'm assuming that light whose energy lies within a specific range is absorbed. You'll note that we can't get green using this method because you'd have to absorb high energy and low energy light without absorbing medium energy light.
This video makes more sense in the context of k-cells, which are boxes with some mathematical formalism that makes them useful for doing integrals. In particular there is a direct formula for calculating the boundary of a k-cell and this boundary follows all the normal properties of things like boundaries.

It always helps to have a formal definition of the boundary of a region, and Topology has us covered. The image explains everything in enough detail that I don't feel a need to go any further here. If you'd like to go further, check out An Intro to Topology.
This one was difficult to make until I figured it out. In it, we glue together two boxes and have the edges of the box disappear. There's also a bit of glowing here so it kind of looks like it's getting fused. I would have liked to maybe do a bit more with it so it looks like the light is moving around, but it will do for what it is.
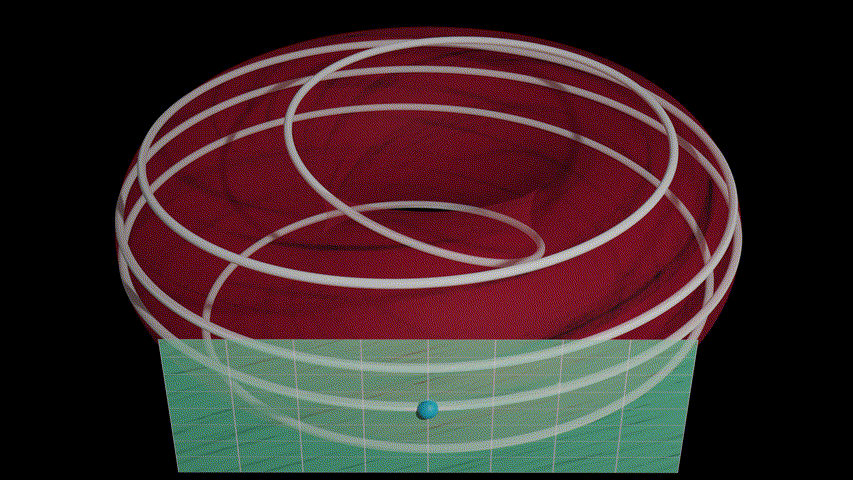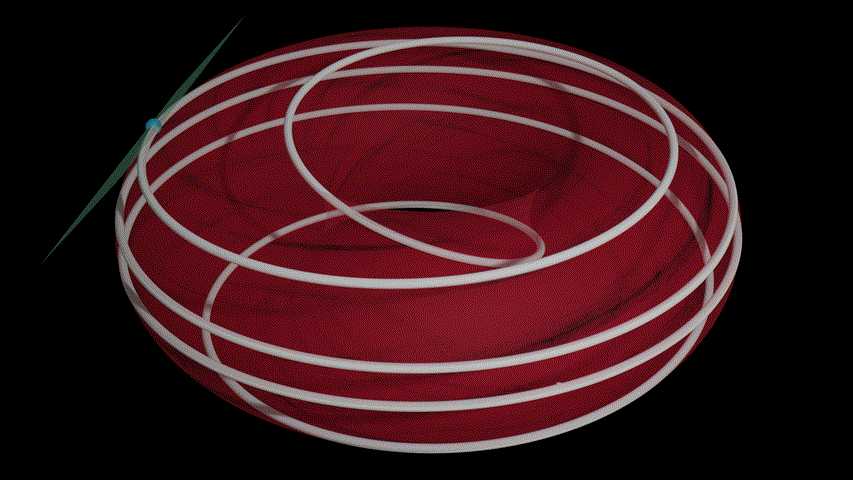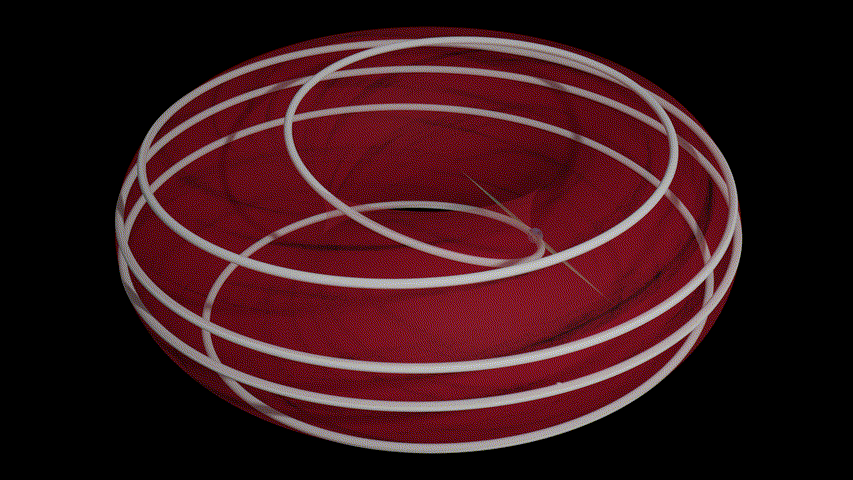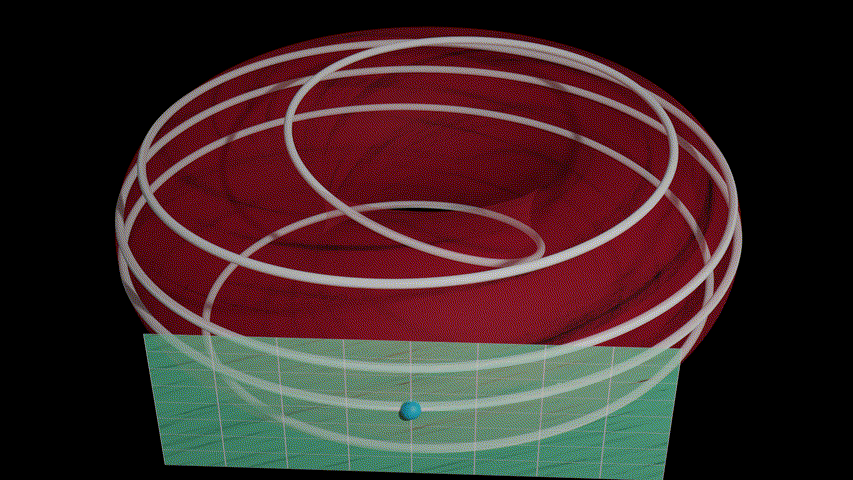
Blender's python scripting system is incredibly powerful, so it's a shame that I don't see a lot of people using it. Here, I generated a curve from a list of points, I move a sphere along that curve along with its local tangent space (more technically there's a tangent space for every point on the manifold and I'm just displaying the one that corresponds to the current point, but you'll have to read Vectors and Covectors for more information). Of particular note is the scaling of the tangent space to get larger or smaller as it moves around the torus. It's pretty funny to me that it's actually easier to get working by understanding a matrix in terms of where you send the basis vectors since it's easy enough to get the local basis vectors of the tangent space, which gives me the correct transformation matrix.
This one was probably one of the hardest videos to make. I had a few textures for the Earth and I wanted to make them pop out like you were peeling them off. If you can show that, it means that the surface of the Earth is a manifold since you can find open sets that can be mapped to Euclidean space. I got that effect, but I had to do some spherical coordinate transformations to move the texture around for each disc.

This image is kind of funny because it's one of my least favorite images in terms of the concept it's supposed to represent (If I could have made An Intro to Tensors without a thumbnail, I would have) , but it's one of my favorite images both aesthetically and technically. To make this image, I had to figure out how to load an arbitrary (both in terms of the position and direction) vector field into Blender. To pull this off, I wrote a script that would let me do so. It also supports animated vector fields, but it's not perfect. I need to get more practice with Blender before I can get it fully set up, but it's good enough for me now.